raadsels en puzzels - rdzl | trap verven raadsel uitleg

Om bij de voordeur van het huis van de professor te komen moet je eerst een trap van twintig treden oplopen. De professor vindt de trap maar saai en besluit om de trap te gaan verven. Hij haalt twee kleuren verf op, groen en geel.

Iedere trede krijgt een groene of gele kleur en bovendien wil de professor dat er geen twee opeenvolgende treden de gele kleur krijgen. Op hoeveel manieren kan de professor zijn trap schilderen? En hoe heet de professor?

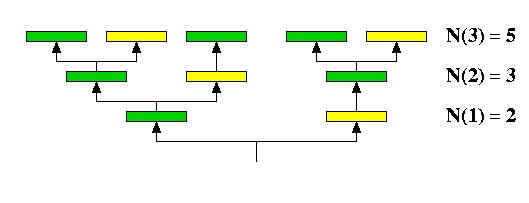
Stel dat de trap uit een trede bestaat. De trap kan dan op twee manieren worden geverfd, zie figuur.
Als de trap uit twee treden bestaat zijn er drie mogelijkheden.
Als de trap uit drie treden bestaat zijn er vijf mogelijkheden.

Na iedere gele trede komt een groene trede.
Na iedere groene trede komt een gele of een groene trede.

Noem het aantal mogelijkheden waarop een trap van x treden geverfd kan worden N(x). Het is gemakkelijk in te zien dat de laatste trede van een trap met x treden op N(x-1) manieren groen kan worden geverfd. De laatste trede van een trap met x - 1 treden kan op N(x-2) manieren groen worden geverfd. Hieruit volgt dat de laatste trede van een trap met x treden op N(x-2) manieren geel kan worden geverfd.

Dus een trap van x treden kan op N(x) = N(x-1) + N(x-2) manieren worden geverfd.

Uit de figuur volgt dat: N(1) = 2 en N(2) = 3.
Hieruit volgt dat:

x	1	2	3	4	5	6	7	8	9	10
N(x)	2	3	5	8	13	21	34	55	89	144

Een kleine berekening laat zien dat N(20) = 17711. De professor kan de trap dus op 17711 manieren verven. Zo'n reeks heet een Fibonaci reeks, naar een Italiaans wiskundige. Waarschijnlijk heet de professor dus Fibonaci.